
Programação
A álgebra é fundamental na programação de computadores, pois muitos algoritmos dependem de operações matemáticas para funcionar de maneira eficiente.
A álgebra é o ramo da matemática que generaliza a aritmética. Isso quer dizer que operações comuns na aritmética (adição, subtração, multiplicação, divisão etc.) serão testados e sua eficácia será comprovada para todos os números pertencentes a determinados conjuntos numéricos. Sendo mais específico, questões como equações, operações, funções, polinômios e estruturas algébricas.
A origem da álgebra teve seu início na Mesopotâmia, onde antigos conhecedores da área desenvolveram técnicas para resolver equações lineares e quadráticas. O papiro antigo de Rhind é um grande exemplo desse trabalho inicial. Usando símbolos e representações geométricas, esses matemáticos resolveram problemas práticos, como a divisão da Terra. Al-Khwarizmi, um matemático do século IX, desempenhou um papel crucial na difusão da álgebra no mundo islâmico e depois na Europa. A álgebra teve evolução na idade média, tendo estudiosos árabes e europeus contribuindo para o desenvolvimento da trigonometria e da álgebra simbólica. O trabalho de François Viète, matemático francês do século XVI, foi fundamental nesse processo. Seu livro “In Artem Analyticam Isagoge” notações dinâmicas algébricas e expandiu o escopo da álgebra. Além disso, René Descartes desenvolveu a geometria analítica, o que também contribuiu para a evolução da álgebra.
No século XIX, a álgebra abstrata e a teoria dos grupos emergiram como áreas de pesquisa matemática de vanguarda. Evariste Galois, um jovem matemático francês, revolucionou a álgebra ao desenvolver a teoria dos grupos, lançando as bases para a álgebra moderna. Seu trabalho, embora não muito reconhecido durante sua vida, teve um impacto duradouro na matemática. Atualmente, a álgebra é uma parte essencial do currículo matemático em todo o mundo, do ensino fundamental ao superior. Autores como Michael Artin, em seu livro “Álgebra”, e David C. Lay, em “Álgebra Linear e suas Aplicações”, contribuíram para tornar a álgebra acessível e relevante para os estudantes. A sua origem etimológica prende-se com o fato de que, nos tempos de outrora, se chamava álgebra à arte que visava reduzir os ossos deslocados ou fracturados/partidos. Porém, este significado caiu em desuso.
Hoje em dia, entende-se por álgebra o ramo da matemática que estuda as estruturas, as relações e as quantidades. Nos estudos de álgebra, letras são utilizadas para representar números. Essas letras tanto podem representar números desconhecidos quanto um número qualquer pertencente a um conjunto numérico. Se x é um número par, por exemplo, então x pode ser 2, 4, 6, 8, 10, .... .... Dessa maneira, x é um número qualquer pertencente ao conjunto dos números pares e fica evidente o tipo de número que x é: um múltiplo de 2.
ASSOCIATIVIDADE
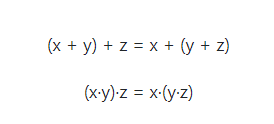
A propriedade associativa nos diz que se você está multiplicando três ou mais números, é possível associar os fatores de maneiras diferentes e mais convenientes.
COMUTATIVIDADE
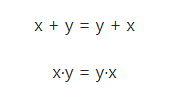
A propriedade comutativa define que não importa a ordem dos valores que você está multiplicando. Pode trocar a ordem que o resultado é o mesmo. Sempre irá garantir que a x b = b x a
DISTRIBUTIVIDADE
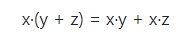
A propriedade distributiva é utilizada quando um número está multiplicando uma adição ou subtração. Basta multiplicar separado cada termo e, somar ou subtrair o resultado. Uma dica importante é colocar em evidência.
Esse é um procedimento, uma ferramenta matemática muito importante. É o caminho inverso da distribuição. Quando você distribui, é o caminho de ida e quando você coloca em evidência, faz o caminho de volta. Realmente, você volta ao ponto em que estava e isso pode parecer desnecessário, mas, não é. Na verdade, é fundamental.

A álgebra é fundamental na programação de computadores, pois muitos algoritmos dependem de operações matemáticas para funcionar de maneira eficiente.

A álgebra desempenha um papel importante nas finanças, ajudando a tomar decisões financeiras mais precisas. Um exemplo comum é o cálculo de juros.

A álgebra, embora pareça distante da culinária, também pode ser aplicada na cozinha. Um exemplo comum é o ajuste de receitas.

A álgebra é fundamental na ciência de dados, fornecendo a base matemática para muitos algoritmos e técnicas utilizadas para análise e modelagem de dados.
Somos uma equipe focada em inovação e criatividade, buscando sempre as melhores soluções para os nossos clientes.
Nossa missão é desenvolver tecnologias que facilitam a vida das pessoas e proporcionam grandes experiências.
Com um time altamente qualificado, nossa equipe está sempre preparada para enfrentar novos desafios.
Estamos comprometidos com a excelência e a entrega de soluções inovadoras para o mercado.